对于数据结构中的链表、二叉树、队列的学习笔记。
链表
基本概念
- 定义1——链表是由一组不必相连【不必相连:可以连续也可以不连续】的内存结构 【节点】,按特定的顺序链接在一起的抽象数据类型。
- 定义2——链表是一种递归的数据结构,它或者为空(null),或者是指向一个结点(node)的引用,该节点还有一个元素和一个指向另一条链表的引用。
分类
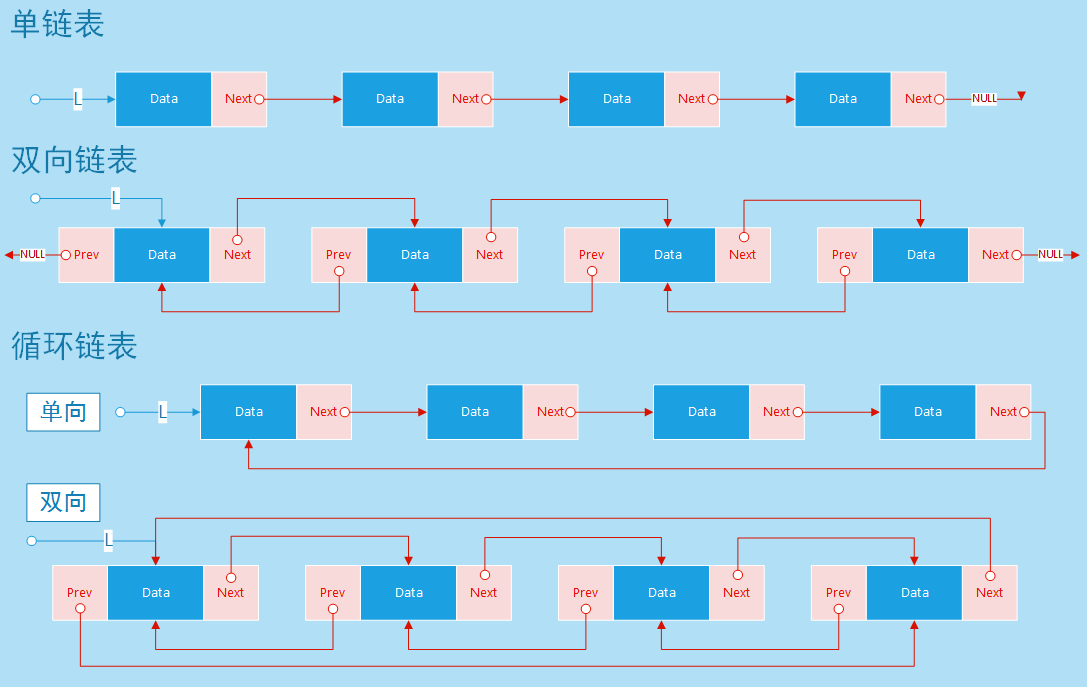
- 单链表
- 双向链表
- 循环链表
基本操作
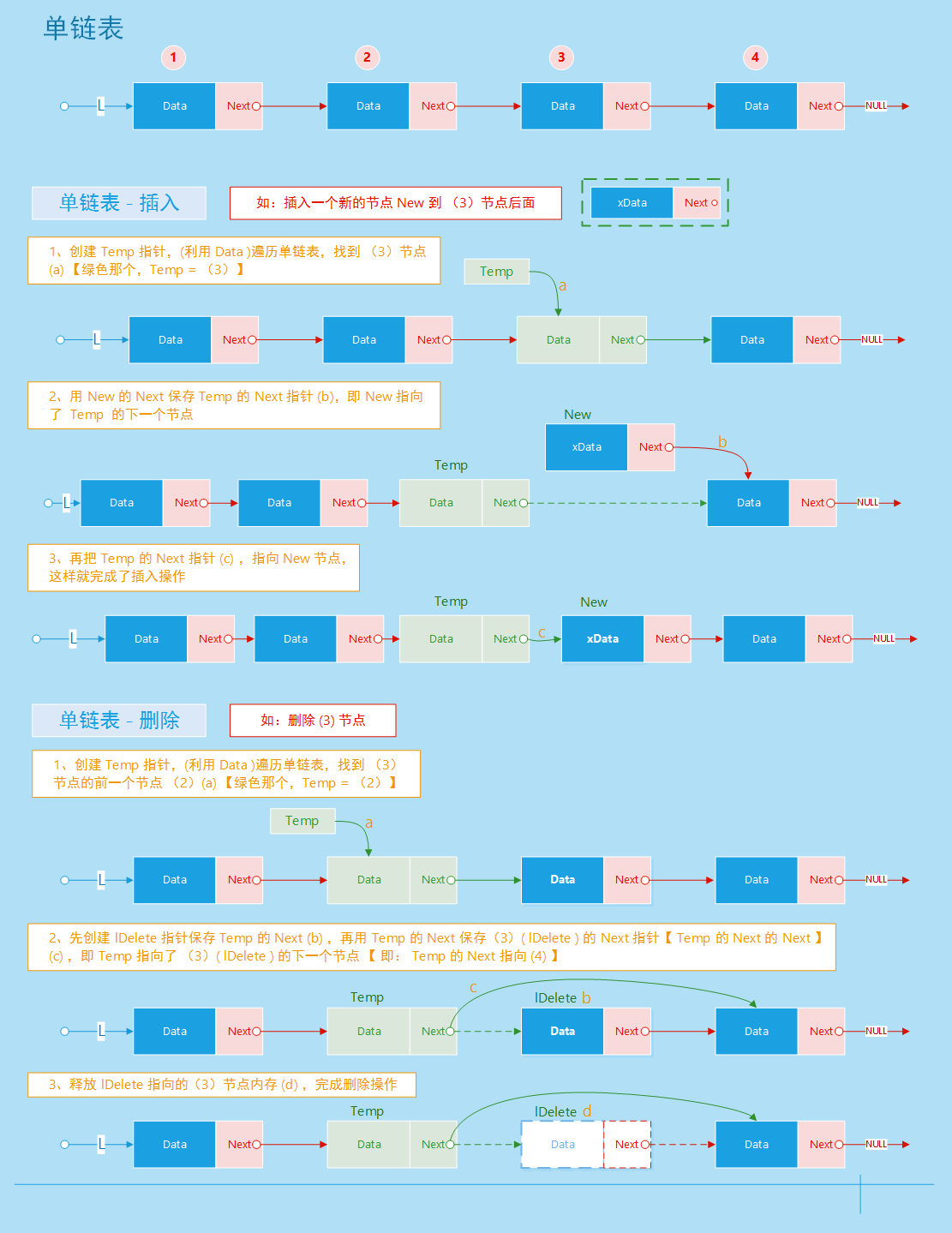
- 插入
- 删除
- 查找【遍历】
单链表操作
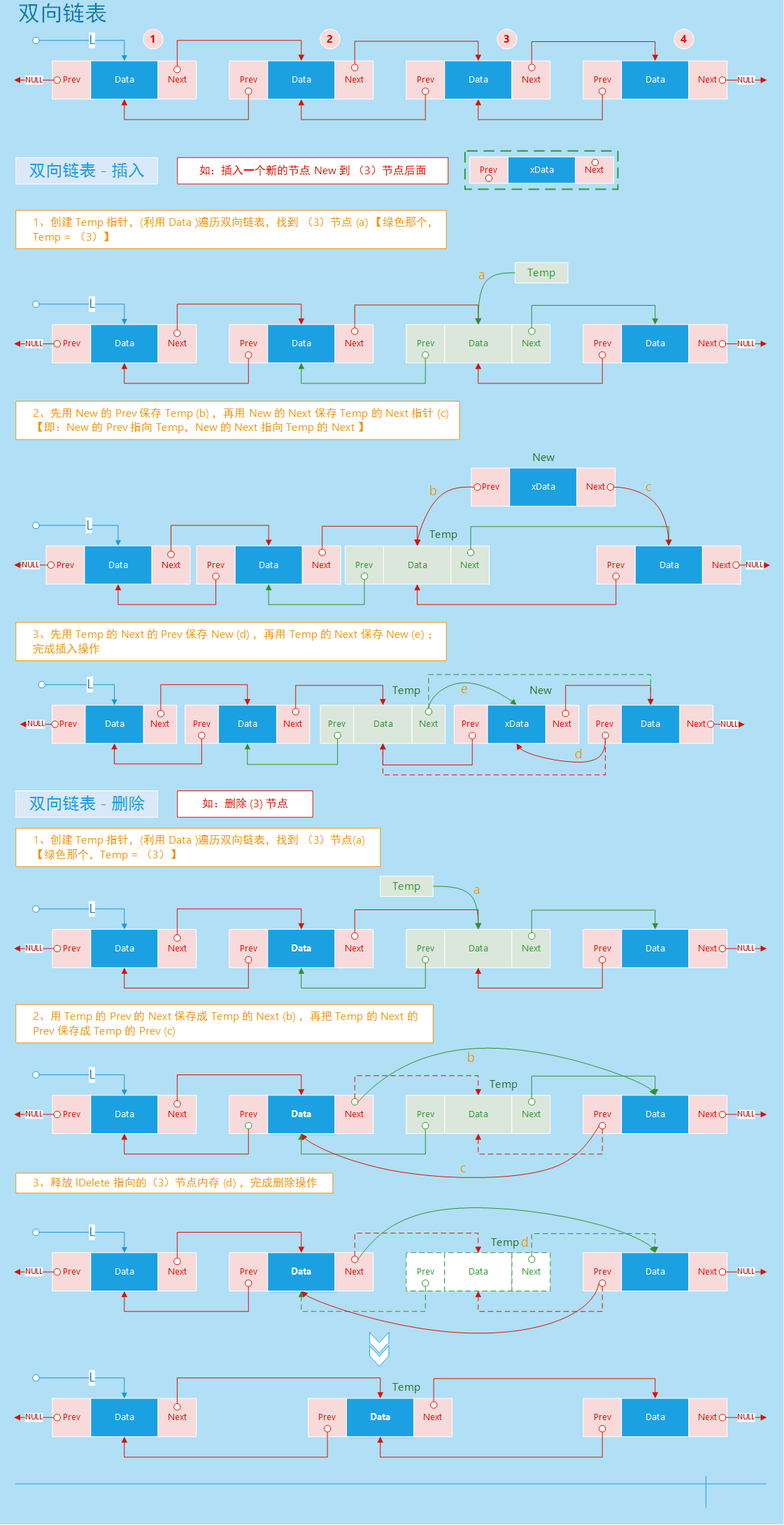
双链表操作
循环链表操作
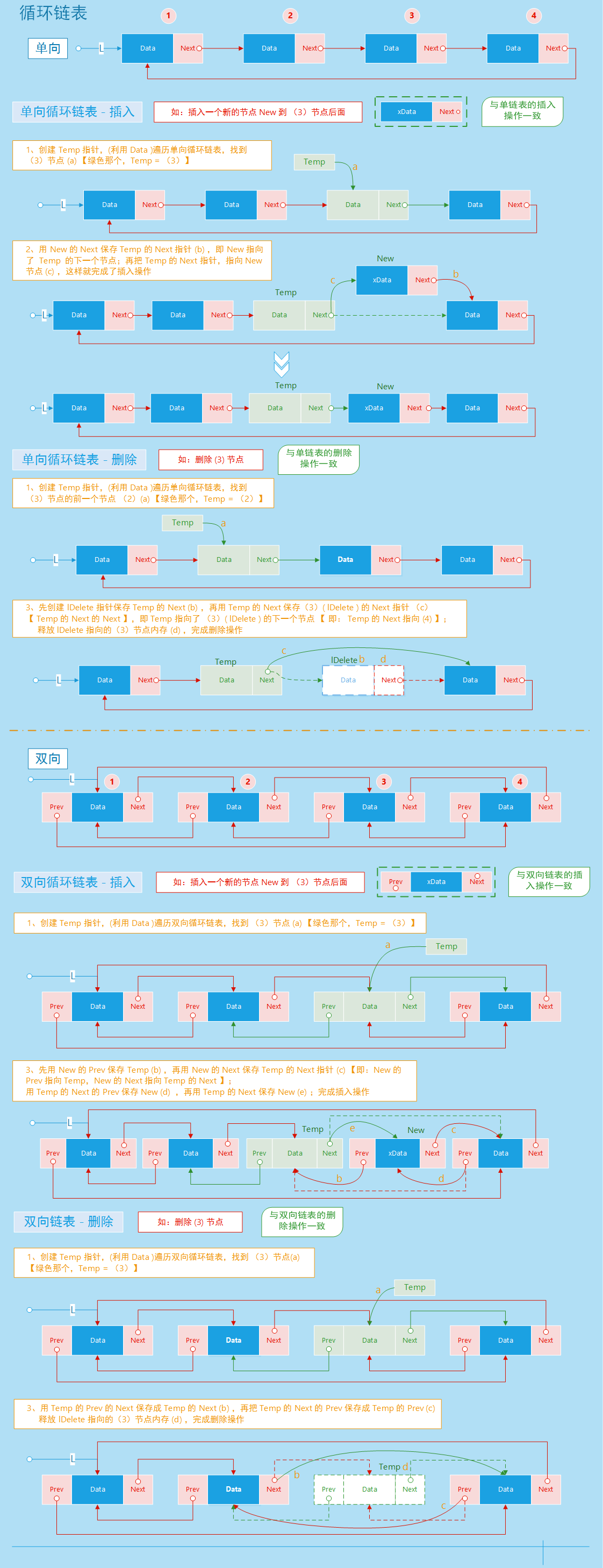
优缺点
优点
- 插入及删除操作的时间复杂度为O(1)。
- 可以动态改变大小。
缺点
由于其链式存储的特性,链表不具备良好的空间局部性,也就是说,链表是一种缓存不友好的数据结构。其不支持高效的random access(随机访问)。
参考资料
二叉树
基本概念
树
树t是一个非空的有限元素的集合,其中一个元素为根,余下的元素组成t的子树。
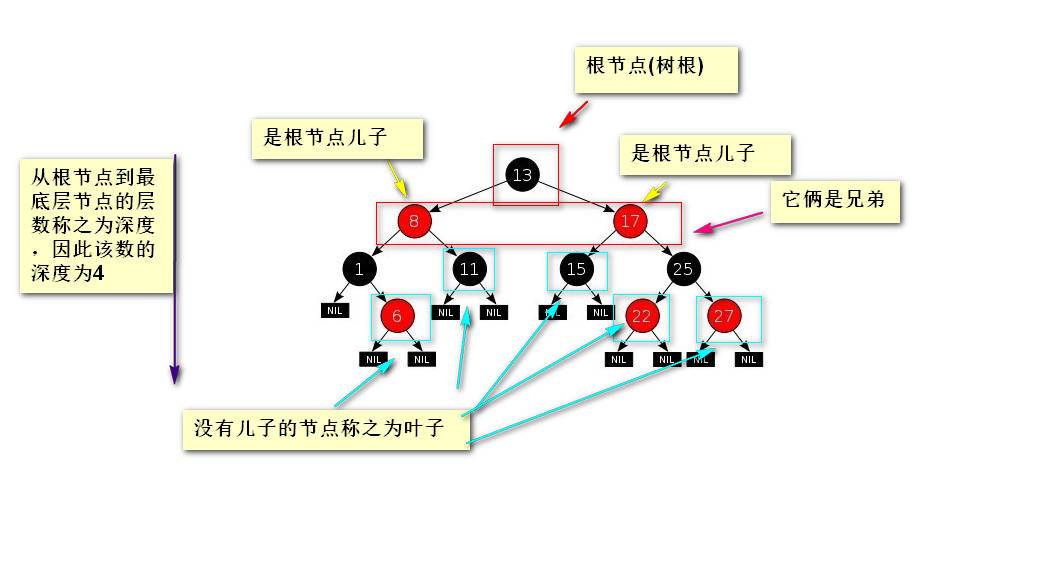
二叉树
二叉树(binary tree)t是有限个元素的集合(可以为空)。当二叉树非空时,其中有一个称为根的元素,余下的元素(如果有的话)被组成2个二叉树,分别称为t的左子树和右子树。
二叉树和树的根本区别
- 二叉树可以为空,树不能为空
- 二叉树中每个元素都恰好有两棵子树(其中一个或两个可能为空)。而树中每个元素可以有若干子树。
- 在二叉树中每个元素的子树都是有序的,也就是说,可以用左、右子树来区别。而树的子树间是无序的。
分类
- 满二叉树(每一个非叶子节点都存在左右子树,并且二叉树中所有的叶子节点都在同一层中)
- 完全二叉树(对于一棵具有n个节点的二叉树按照层次编号,同时,左右子树按照先左后右编号,如果编号为i的节点与同样深度的满二叉树中编号为i的节点在二叉树中的位置完全相同,则这棵二叉树称为完全二叉树。)
- 二叉查找树(当前根节点的左边全部比根节点小,当前根节点的右边全部比根节点大。往往我们动态创建二叉树都是创建二叉查找树。)
完全二叉树——
二叉查找树——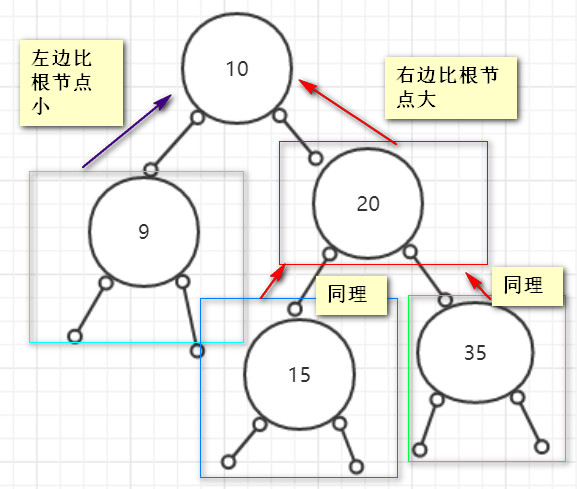
基本操作
存储结构
在实际使用中,根据不同的需要,使用顺序存储结构和链式存储结构。对于链式存储结构,我们定义如下——
typedef struct BiNode{
int data;// 数据域的值
struct BiNode *left;// 左孩子
struct BiNode *right;// 右孩子
}binode;
二叉树的遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 逐层/层次遍历(用链表存储每一层的节点,同时,遍历完一个节点,将其左右子节点增加进链表中。)

参考资料
队列
基本概念
队列是一种先进先出(First In First Out)的线性表,简称FIFO。它是一种只允许在一端进行插入操作,而在另一端进行删除操作的线性表。 允许插入的一端称为队尾,允许删除的一端称为队头。
分类
顺序存储结构(顺序队列)
采用环状顺序表来存放队列元素,并用两个指针,其中 front 指针指向队列的队头元素,rear指针指向队尾元素的下一个位置,往队列中加进或取出元素时分别改变这两个变量的计数。当头尾指针(front / rear)指向队列尾的元素(下标:QueueSize-1)时,其加1操作的结果是指向向量的下界0。
特殊情况的判定——空\满队列
当队列为空或者满的时候都会出现 front == rear 的情况,即无法通过条件 front == rear 来判别队列是”空”还是”满”。解决这个问题的方法至少有三种。
- 另设一布尔变量或标志变量以区别队列的空和满;
- 保留一个元素空间。约定入队前,测试对尾指针 rear 在循环意义下加1后是否等于 front,若相等则认为队满(注意:rear所指的单元始终为空),此时判空条件仍是 front == rear,判满条件改变;
- 使用一个计数器记录队列中元素的总数(即队列长度)。
链式存储结构(链队列)
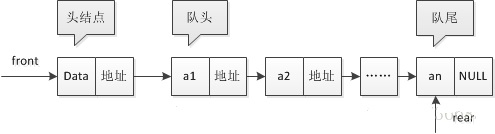
其实就是线性表的单链表,只是它只能对尾进,队头出。并且规定队头指针指向链队列的头结点,对尾指针指向终端节点,当队列为空时,front和rear都指向头结点。
入队操作,就是在链表尾部插入结点;出队操作就是头结点的后继结点出队,然后将头结点的后继后移。如果最后除了头结点外,只剩一个元素了,就把rear也指向头结点。
非空链队列如下图所示。