对于常用算法中的递归、分治、动态规划、贪心算法、回溯法、深度优先搜索、广度优先搜索算法的学习笔记。
递归
基本概念
递归算法是一种直接或者间接调用自身函数或者方法的算法。
通俗来说,递归算法的实质是把问题分解成规模缩小的同类问题的子问题,然后递归调用方法来表示问题的解。它有如下特点:
- 一个问题的解可以分解为几个子问题的解。
- 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样。
- 存在递归终止条件,即必须有一个明确的递归结束条件,称之为递归出口。
经典示例
- 数组求和
- 汉诺塔(Hanoi Tower)问题
- 爬台阶问题
如何写递归代码
- 找到如何将大问题分解为小问题的规律。
- 通过规律写出递推公式。
- 通过递归公式的临界点推敲出终止条件。
- 将递推公式和终止条件翻译成代码。
分治算法
基本概念
对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
因为在求解大问题时,需要递归的求小问题,因此一般用递归的方法实现,即自顶向下。
适用情况

经典示例
- 二分搜索
- 大整数乘法
- Strassen矩阵乘法
- 棋盘覆盖
- 合并排序
- 快速排序
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
如何设计程序
实际上就是类似于数学归纳法,找到解决本问题的求解方程公式,然后根据方程公式设计递归程序。
- 一定是先找到最小问题规模时的求解方法;
- 然后考虑随着问题规模增大时的求解方法;
- 找到求解的递归函数式后(各种规模或因子),设计递归程序即可。
递归与分治
- 分治策略用于解决原问题与子问题结构相似的问题,对于各子问题相互独立的情况,一般用递归实现。
- 递归是实现手段,分治策略是解决问题的思想。
动态规划算法
基本概念
- 动态规划其实和分治策略是类似的,也是将一个原问题分解为若干个规模较小的子问题,递归的求解这些子问题,然后合并子问题的解得到原问题的解。
- 区别在于这些子问题会有重叠,一个子问题在求解后,可能会再次求解,于是我们想到将这些子问题的解存储起来,当下次再次求解这个子问题时,直接拿过来就是。
- 动态规划所解决的问题是分治策略所解决问题的一个子集,只是这个子集更适合用动态规划来解决从而得到更小的运行时间。
- 用动态规划能解决的问题分治策略肯定能解决,只是运行时间较长。因此,分治策略一般用来解决子问题相互对立的问题,称为标准分治,而动态规划用来解决子问题重叠的问题。
基本实现
- 动态规划一般由两种方法来实现,一种为自顶向下的备忘录方式,用递归实现,一种为自底向上的方式,用迭代实现。
- 在自顶向下的动态规划中,我们存储已知的值;在自底向上的动态规划中,我们预先计算这些值。
适用条件

求解的基本步骤

递归、分治与动态规划
- 动态规划用于解决子问题有重复求解的情况,既可以用递归实现,也可以用迭代实现;
- 递归是实现手段,分治策略是解决问题的思想,动态规划很多时候会使用记录子问题运算结果的递归实现。
贪心算法
基本概念
贪心算法(greedy algorithm),又称贪婪算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。比如在旅行推销员问题中,如果旅行员每次都选择最近的城市,那这就是一种贪心算法。
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。简单地说,问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
贪心法可以解决一些最优化问题,如:求图中的最小生成树、求哈夫曼编码……对于其他问题,贪心法一般不能得到我们所要求的答案。一旦一个问题可以通过贪心法来解决,那么贪心法一般是解决这个问题的最好办法。由于贪心法的高效性以及其所求得的答案比较接近最优结果,贪心法也可以用作辅助算法或者直接解决一些要求结果不特别精确的问题。
基本思路
- 建立数学模型来描述问题。
- 把求解的问题分成若干个子问题。
- 对每一子问题求解,得到子问题的局部最优解。
- 把子问题的解局部最优解合成原来解问题的一个解。
适用情形
贪心策略适用的前提是:局部最优策略能导致产生全局最优解。
实现框架
从问题的某一初始解出发;
while (能朝给定总目标前进一步)
{
利用可行的决策,求出可行解的一个解元素;
}
由所有解元素组合成问题的一个可行解;
贪心算法与动态规划
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
回溯算法
基本概念
类似于枚举,通过尝试遍历问题各个可能解的通路,当发现此路不通时,回溯到上一步继续尝试别的通路。
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
基本实现
- 针对所给问题,确定问题的解空间:首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。
- 确定结点的扩展搜索规则
- 以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
算法框架
- 非递归回溯框架
- 递归的算法框架
回溯与深度优先搜索
- 回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单。
- 回溯是深度优先搜索的一种特例,它在一次搜索过程中需要设置一些本次搜索过程的局部状态,并在本次搜索结束之后清除状态。而普通的深度优先搜索并不需要使用这些局部状态,虽然还是有可能设置一些全局状态。
深度优先搜索DFS(Depth-First-Search)
基本概念
深度优先搜索是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。
深度优先搜索(缩写DFS)有点类似广度优先搜索,也是对一个连通图进行遍历的算法。它的思想是从一个顶点V0开始,沿着一条路一直走到底,如果发现不能到达目标解,那就返回到上一个节点,然后从另一条路开始走到底,这种尽量往深处走的概念即是深度优先的概念。
算法步骤
深度优先遍历图算法步骤如下——
- 访问顶点v;
- 依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
- 若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
广度优先搜索BFS(Breadth-First-Search)
基本概念
从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止。BFS同样属于盲目搜索。一般用队列数据结构来辅助实现BFS算法。
算法步骤
- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。如果找到目标,则结束搜寻并回传结果。否则将它所有尚未检验过的直接子节点加入队列中。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
- 重复步骤2。
DFS与BFS
对比
广度优先搜索
在树的层次较深&子节点数较多的情况下,消耗内存十分严重。广度优先搜索适用于节点的子节点数量不多,并且树的层次不会太深的情况。
深度优先搜索
难以寻找最优解,仅仅只能寻找有解。其优点就是内存消耗小,克服了刚刚说的广度优先搜索的缺点。
实例
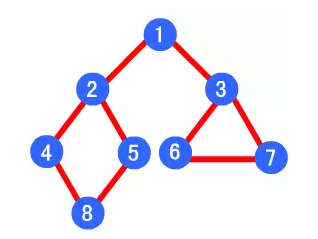
如下图,其深度优先遍历顺序为 1->2->4->8->5->3->6->7;其广度优先算法的遍历顺序为:1->2->3->4->5->6->7->8.
总结
策略是面向问题的,算法是面向实现的。
算法策略间的关系

算法策略侧重的问题类型
一般常遇到的问题分为四类:
- 判定性问题:可用递推法、递归法
- 计算问题:可用递推法、递归法
- 最优化问题:贪心算法、分治法、动态规划法、枚举法
- 构造性问题:贪心算法、分治法、广度优先搜索、深度优先搜索
参考资料
关于递归、分治以及动态规划
递归和动态规划
递归、分治策略、动态规划以及贪心算法之间的关系
看动画轻松理解「递归」与「动态规划」
五大常用算法之一:分治算法
五大常用算法之二:动态规划算法